Thanks for the comments!
And sorry, it's clear that the way my final expression displays makes its meaning ambiguous. The expression in block parenthesis is not meant to be part of the exponent. Perhaps this makes the integral clearer
 + d - 1}{d} \right]^M$)
Does that look any more analytically approachable to anyone? Meh, it probably doesn't matter since my result doesn't hold for anything more than d=1.
It's a little unclear to me how I would find a theoretical average for
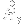
which is why I haven't used my first integral directly. I simply don't know how to compute it. This is why I introduced the
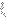
variables. Perhaps I could compute the average of R by assuming it to be a sum of the
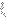
and using the central limit theorem, but then I need both the average and standard deviation of my
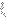
. It's also completely possible that what I'm saying is complete gibberish right now, I'm just thinking out loud.
I'm unfamiliar with stochastic integrals, and what difficulties might be introduced when replacing
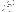
with
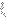
. I figured that the process is okay, though, since by definition
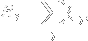
and therefore

My suspicion is also that my calculation for the average of the exponential is wrong. One possible pitfall in my model is that for fixed j the
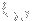
are not independent, since only one member of that subset can be nonzero, which I have not accounted for explicitly. I know that for random variables there are sometimes extra terms that need to be added for certain operations that you wouldn't expect, i.e
 = M(A) + M(B) - M(A \cap B))
where M is the measure of a set. The last term comes up somewhat unexpectedly unless you've thought about that kind of operation before. I'm not sure if there might be something like that in the computation of the exponential average that I might not have accounted for. That's something I can look into.
The alternative solution I'm considering trying is to decompose my R vector a little differently. I'm thinking of having a single
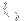
per step ranging from 1 to 2d. I can then write
} - \delta_{(\xi_j, 2i)})
.
This means that
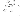
would increment by +1 if

and -1 if
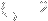
,
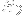
would increment by +1 if
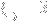
and -1 if
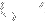
and so on. This should decompose my R correctly as far as I can tell, and should get rid of any dependency issues that come up since there is only one
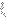
per step. I'll try this later today and let you know if it works. I'll also look into how to calculate the average of a sum of mutually dependent variables.
Thanks again, guys.


 Similar Threads
Similar Threads
