The integral seems fine for d=1 (both for obvious inputs, like a probability of 1/2 for the point x=1 after one step, and less obvious ones simulated by your program).
For d=2 dimensions, a simple case for which the distribution seems to fail is the point
)
and M=2 steps, which should yield a probability of 1/8 (each walk corresponds to a word of length 2 in the alphabet {U,D,L,R}. There are 16 such words in total, of which only UR and RU correspond to a desired walk). In this case, the integral becomes
 + 1}{2}\right]^2\mathrm{d}q_i = \frac{1}{4})
for
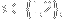
so the product is
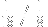
Actually, this seems like a pretty fun problem to solve by counting words...
"Stephen Wolfram is the creator of Mathematica and is widely regarded as the most important innovator in scientific and technical computing today." - Stephen Wolfram