I tried using my new expansion for R. Got the same result, as expected. I figured I'd carry out the math though to check for the possibility of there being some hidden term or factor that pops out. So, either my final integral in the original post is correct or I'm messing up my expectation algebra somewhere.
For some reason I never considered doing a multinomial expansion, but that definitely seems to be the way to go. Your evaluation of the integral even appears like what I'd expect the combinatoric solution to be, which is promising. I'm wondering if perhaps I messed up entering my integral expression into the numerical integrator.
Could someone else possibly check the final numerical integral in the original post for me using
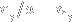
, where
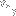
is the ith point on the lattice whose probability we're looking for. Just to make sure I'm not doing something incredibly stupid. I will post some code that the numerical evaluation can be checked against.
The code is as follows
Code:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main(void)
{
int trialPoint[] = {1,1,1,1}; // Enter the point whose probability you want to find
int maxStep = 10; // Maximum number of steps per walk
int trials = 10000000; // Number of walks
int dimension = sizeof(trialPoint)/sizeof(trialPoint[0]); // lattice dimension
int lattice[dimension]; // Holds the value of where you are in each component of lattice
srand(time(NULL));
int counter = 0; // Holds number of trials that end at desired point
for(int trial = 0; trial<trials; trial++)
{
for(int i = 0; i<dimension; i++) // Sets initial position on lattice to (0,0,0,...)
{
lattice[i]=0;
}
// Following segment of code steps forward or backwards in a single dimension per loop
for(int step = 0; step<10; step++)
{
int forwardBackward = rand()%2;
int component = rand()%dimension;
if(forwardBackward==1)
{
lattice[component]++;
}
else
{
lattice[component]--;
}
}
// Check to see if end-position on lattice is desired position set in trialPoint array
// If so, counter variable is incremented
int match = 1;
for(int i = 0; i<dimension; i++)
{
if(lattice[i]!=trialPoint[i])
{
match = 0;
break;
}
}
if(match == 1)
{
counter++;
}
}
printf("%d/%d simulated probability\n", counter, trials);
return 0;
} |
This code simulates the random walk. The only thing you should need to modify in the code is if you want to change the trial point, you can do so in the first line in the main function. The code can handle arbitrary dimensions, so feel free to change it to any dimension as needed. You can also modify the number of steps a walk takes per trial and the total number of trials in the following two lines respectively. Note, that the code assumes that the trial point is the lattice-point number with respect to the origin, and doesn't take the lattice constant a into consideration. That is why I recommend evaluating the following integral:
 + d - 1}{d} \right]^M.)
All you have to do is supply the
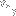
, where
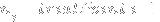
i.e. and so on. The i in the exponential of the integral is indeed the imaginary unit. If someone could run my code and compare the answer with the numerical integral provided above, it'd be much appreciated. When I tried it, the answers did not coincide except for d=1. Also, M in the equation is maxStep from the code, and d is dimension of the lattice.