|
Not at all what I expected. Then I looked closer at your statement and discovered all the golden ratios. Always knew that the ratio of successive terms in the fibonacci sequence tended to the golden ratio, but didn't realize that you could actually generate fibonacci terms that way. Pretty cool.
|
I'm glad you liked it! Yes, linear recurrence relations like

lend themselves well to explicit solutions by the transformation
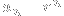
, but to be fair, there aren't really
that many examples of them of order
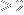
that are interesting. Nonlinear ones, such as the logistic map
,)
become very interesting and intractable very quickly, though:
https://www.youtube.com/watch?v=ovJcsL7vyrk
Personally, I think the weird connections between recurrence relations, differential equations, generating functions and derivatives are particularly fascinating. For example, the
Legendre polynomials )
(which have a very large number of applications in physics, probability theory, etc) can be defined in either of the following four ways:
1. In terms of a recurrence relation (with
 = 1,\,P_1(x) = x)
):
 P_{n+1}(x) = (2n+1) x P_n(x) - n P_{n-1}(x))
2. In terms of n-th derivatives:
 = \frac{1}{2^n n!} \frac{\mathrm{d}^n}{\mathrm{d}x^n} \left(x^2 -1\right)^n)
3. As coefficients of a series expansion (from electrostatics):
 t^n)
4. As polynomial solutions of an ordinary differential equation (which you get from solving Laplace's equation in spherical coordinates):
y''(x) - 2xy'(x) + n(n+1)y(x) = 0)
If you play around with various polynomial sequences for a while (particularly
orthogonal sequences), it becomes "obvious" that there's some sort of space or operator that connects all of the above. In other words, it's a bit like there "has to be" some algorithm to convert a differential equation to a recurrence relation, or vice versa, but the general theory for that is very poorly understood.
Also, as a cool sidenote, you can use the zeros
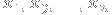
of the n-th Legendre polynomial
)
for numerical integration of many "nice" functions
)
:
\,\mathrm{d}x \approx \sum_{k=1}^{n} \frac{2f(x_k)}{(1-x_k^2)(P'_n(x_k))^2})
Gauss himself came up with that one, obviously...
"Stephen Wolfram is the creator of Mathematica and is widely regarded as the most important innovator in scientific and technical computing today." - Stephen Wolfram


 Similar Threads
Similar Threads
