Random walk in arbitrary dimension

Profile · 06:36 PM

I'm trying to find the probability distribution for a random walk on a lattice with lattice constant a in arbitrary dimension d. The rules for my walk is that in each step the walker has to move to an adjacent spot on the lattice along one and only one component. My logic is as follows.

My probability distribution ought to be

$\reverse \rho^L_{\vec{r}/a, t/\tau} = \langle \delta_{\vec{R}(t), \vec{r}} \rangle.$

Here, [itex]\vec{r}[/itex] is my final position vector from the starting point of the walk, t is the total time since we started the walk and $\tau$ the time per step. [itex]\vec{R}(t)[/itex] is a random variable consistent with the final position of the walk. [itex]L[/itex] simply indicates that we are on a lattice, and is merely included for consistency with my textbook. The delta-function is a d-dimensional delta function, d being the dimensionality of my lattice. Since the delta-function is normalized the right-hand side should represent the probability distribution of my random walk. Using the Fourier representation of a delta function, and the fact that a multidimensional delta-function is a product of single dimensional delta-functions, I can rewrite my probability distribution as

$\reverse \rho^L_{\vec{r}/a, t/\tau} = \langle \prod_{i=1}^d \int_{- \pi}^{\pi} \frac{dq_i}{2 \pi} e^{iq_i(R_i(t)-r_i)/a} \rangle.$

[itex]R_i[/itex] and [itex]r_i[/itex] represent the ith component of my random variable and the ith component of the position on my lattice whose probability I want to find respectively. I can rewrite [itex]R_i[/itex] as follows:

$\reverse R_i = \sum_j^{t/\tau} \xi_{j,i}.$

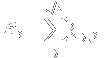
Here, my [itex]\xi_{j,i}[/itex] represent the change in [itex]R_i[/itex] on step j. Writing [itex[M=t/\tau[/itex] my probability distribution is therefore

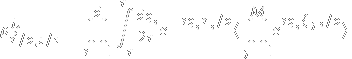
$\reverse \rho^L_{\vec{r}/a, t/\tau} = \prod_{i=1}^d \int_{- \pi}^{\pi} \frac{dq_i}{2 \pi} e^{-iq_ir_i/a} \langle \prod_{j=1}^M e^{iq_i \xi_{j,i}/a} \rangle.$

[itex]\xi_{j,i}/a[/itex] can take on values of +1, 0, or -1 with probability 1/2d, (d-1)/d, and 1/2d respectively. So

$\reverse \langle e^{iq_i \xi_{j,i}/a} \rangle = \frac{e^{iq_i}}{2d} + \frac{d-1}{d} + \frac{e^{-iq_i}}{2d} = \frac{\cos \left( q_i \right) + d - 1}{d}$

$\reverse \rho^L_{\vec{r}/a, t/\tau} = \prod_{i=1}^d \int_{- \pi}^{\pi} \frac{dq_i}{2 \pi} e^{-iq_ir_i/a} \left[ \frac{\cos \left( q_i \right) + d - 1}{d} \right]^M$$

Most of the probability distributions I'v seen for the d-dimensional random walk are based on combinatoric considerations. Can anyone confirm that the logic and final expression for my probability distribution are correct. Also, does anyone have any advice on how to proceed with the final integral? Chruser? WW? Anyone?

Also, I don't know how to do inline latex on Zelaron

Can one of you guys fix my post for me so that the inline latex shows up?

Thread Tools
Show Printable Version Email this Page
Display Modes
Switch to Linear Mode Switch to Hybrid Mode Threaded Mode

Similar Threads
Thread	Thread Starter	Forum	Replies	Last Post
Random 35 Tracks Tape.	Mdselctr	Science and Art	1	2009-09-24 05:59 PM
Random Title	Chruser	Forum News, Suggestions and Discussion	29	2002-05-14 09:16 PM

Currently Active Users Viewing This Thread: 1 (0 members and 1 guests)