This one is fun to think about
:
The two envelope problem is a famous paradox from probability theory (which we first presented on Plus back in September). Imagine you are given two envelopes, one of which contains twice as much money as the other. You're allowed to pick one envelope and keep the money inside. But just before you open your chosen envelope you are given the chance to change your mind. Should you stick with the envelope you picked first or switch?
To find out write
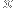
for the amount that's in your chosen envelope. This means that the amount of money in the other envelope is either
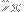
or
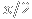
. The probability that it's
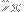
is
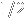
and so is the probability that it's
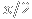
. So the expected amount you'll get for switching is
 =x+\frac{x}{4} = \frac{5x}{4}. )
Since that’s bigger than
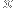
. But it's intuitively obvious that switching shouldn't increase your expected value, since you haven't been given any new information. Furthermore, after switching you could make the exact same argument and conclude you should switch again, ad infinitum. So there's a paradox here and the problem is to resolve it.


 Similar Threads
Similar Threads
