I've found a number of closely related functions, each of which takes three complex numbers
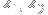
, and
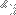
(which we can consider as the vertices of a triangle) as its arguments, and outputs a complex number
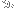
. A few of these functions represent well-known triangle centers
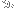
, such as the centroid (that is,
/3))
), or the zeros and critical points of the polynomial
 = (z-z_1)(z-z_2)(z-z_3))
. Other functions among them are less obvious, such as the following point

:
 z_1^2+\left(z_2^2-6 z_3 z_2+z_3^2\right) z_1+z_2 z_3 (z_2+z_3) \sqrt{-3(z_1-z_2)^2 (z_1-z_3)^2 (z_2-z_3)^2}}{2 \left(z_1^2+z_2^2+z_3^2-z_1z_2 - z_1z_3-z_2z_3\right)})
As far as I can tell, by comparing the point
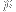
to different triangle centers in
GeoGebra Classic 6, it seems to be the
first isodynamic point to a high degree of precision for all triangles that I've thrown at it so far. My problem is twofold:
)
How do I prove that
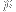
is (or isn't) the first isodynamic point of the triangle
)
?
)
How do I (numerically) match
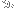
with likely triangle centers based on the
Encyclopedia of Triangle Centers? GeoGebra uses a small portion of the material in the ETC, but unfortunately, it fails to implement some important triangle centers with low indices. Suggestions for other, similar resources are welcome, too.
As for
)
, I think a viable starting point might be to convert
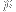
into barycentric or normalized trilinear coordinates and directly compare the result to the coordinates given in the ETC, but I'm not sure how to do this. It seems to be slightly easier to use Cartesian coordinates as a starting point, but Mathematica (for example) generally doesn't seem to be very inclined to return the real and imaginary parts of
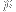
(for general
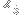
, e.g. when you let
for real numbers
and simplify the expressions).
Regarding
)
, the following website can supposedly be used to compare points to almost all entries in the ETC:
https://faculty.evansville.edu/ck6/e...ch_6_9_13.html
Unfortunately, I seem to get inconsistent results from my attempts to implement the algorithm on the website above in Mathematica. More specifically, certain triangle centers that I've tested (such as the centroid) yield the correct coordinates in the list, while other obvious ones that I've tested are either not listed, or have the wrong index. I suspect that I've misunderstood the information on the website in some elementary way, so feel free to correct my algorithm (for
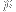
above, in the example that follows):
)
Choose
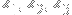
as the vertices of a triangle with side lengths
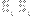
and
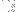
, e.g.
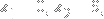
and
 + (8/9)\sqrt{35}i)
.
)
Solve the following linear system of equations for
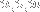
:
 + v\,\text{Re}(z_2) + w\,\text{Re}(z_3) = \text{Re}(p))
 + v\,\text{Im}(z_2) + w\,\text{Im}(z_3) = \text{Im}(p))
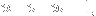
where
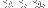
are the barycentric coordinates for
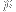
. (Here,
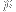
can be approximated to a high degree of precision, e.g. to avoid problems with Mathematica...)
)
Let
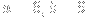
, and
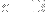
(or, more ideally, just use the Pythagorean theorem...), and define
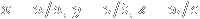
. Furthermore, calculate the area of the triangle as
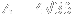
.
)
Calculate
 = 2Ax/(u+v+w))
, which should be the sought "coordinate" in the table.
Carrying out the algorithm above yields
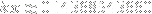
, whereas the coordinate for the first isodynamic point (with index
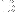
in the table) is
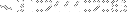
. Perhaps
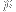
isn't actually the first isodynamic point, but I like to think that I've done something wrong...
"Stephen Wolfram is the creator of Mathematica and is widely regarded as the most important innovator in scientific and technical computing today." - Stephen Wolfram


 Similar Threads
Similar Threads
