Zelaron Gaming Forum - View Single Post

Asamin

Asamin said: [Goto]

Imma go ahead and not copy-paste so d3v can't rage but I would say it's the infinite sum of n

Most of the solution is assumptions based on infinite series (the controversial part is that whatever theorem they taught us that if a sum cycles between two points, it's convergence is the average of those two points) solves to -1/12. So theoretically, if you add up every natural positive number into infinity, you get -1/12.

Wiki if curious. I found this originally from a numberphile video that I'll also link where they do the proof.
Wiki
Numberphile video

Zeta function regularization is fake and gay.

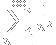
In all seriousness, even though I dislike the 1 + 2 + 3 + ... = -1/12 "identity" that arises from analytic continuation of the Dirichlet series $\reverse \sum_{n=1}^\infty\frac{1}{n^s}$ into the Riemann zeta function $\reverse \zeta(s)$ , the function itself is fantastic. Also, Euler's connection between the Dirichlet series (and thus the Riemann zeta function) and the prime numbers is possibly my favorite equation:

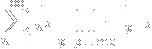
$\reverse \sum_{n=1}^\infty\frac{1}{n^s} = \prod_{p \text{ prime}} \frac{1}{1-p^{-s}}$

You can do all sorts of fun things with it. For instance, let s=1. Then the left-hand side is the harmonic series, which diverges. Thus the right-hand side must also diverge, which can only happen if there is an infinite number of primes. Euclid's proof was rubbish in comparison.